At its core, the compound interest formula is A = P(1 + r/n)^(nt). While that might look like something out of a high school math class, it’s the engine that calculates the future value (A) of your investment by adding interest not just to your initial principal (P), but to all the interest you’ve already earned along the way.
The Snowball Effect: How Compound Interest Works

Think of a small snowball at the very top of a long, snowy hill. Give it a gentle nudge. As it starts rolling, it picks up a little more snow. With every single rotation, it gets slightly bigger, and that larger size helps it grab even more snow on the next turn. Before you know it, that tiny snowball has turned into a massive boulder by the time it reaches the bottom.
That’s the perfect way to visualize compound interest. It’s not just about earning interest on your initial deposit—it’s about earning interest on your interest. Your money grows, and that newly grown amount starts earning its own interest, kicking off a powerful cycle of accelerating growth.
A Tale of Two Savers
To see this in action, let’s imagine two friends, Alex and Ben. Each starts with $10,000 in an account that pays 5% annual interest. The only difference is how that interest is calculated.
Ben’s account uses simple interest. He earns 5% on his original $10,000 every single year. That’s a predictable $500. After 10 years, he’s earned a total of $5,000 in interest ($500 x 10 years), bringing his final balance to $15,000. His growth is a steady, straight line.
Alex’s account uses compound interest. In year one, he also earns $500. But in year two, he earns 5% on his new, slightly larger balance of $10,500. His interest for that year is $525. That extra $25 might not seem like much, but this is where the magic really starts.
Over the years, Alex’s interest payments get bigger and bigger because his principal is constantly growing. This small mechanical difference eventually creates a huge gap between their final account balances. While Ben’s growth is linear, Alex’s is a curve that gets steeper and steeper over time. This is the whole reason the compound interest formula is so crucial to grasp.
Key Takeaway: Simple interest pays you on your starting amount only. Compound interest pays you on your starting amount plus all the interest you've already accumulated, creating exponential growth.
Simple vs Compound Interest At a Glance
The difference between these two methods truly dictates the speed and scale of your financial growth. Getting this distinction right is the first real step toward making your money work harder for you.
Here’s a quick side-by-side comparison.
| Feature | Simple Interest | Compound Interest |
|---|---|---|
| How It's Calculated | Interest is only earned on the original principal amount. | Interest is earned on both the principal and the accumulated interest. |
| Growth Pattern | Linear growth, adding the same amount of interest each period. | Exponential growth, as the interest earned also starts earning interest. |
| Long-Term Potential | Modest and predictable returns over time. | Significant wealth acceleration, especially over longer periods. |
Ultimately, one method adds, while the other multiplies. For anyone serious about growing their savings, understanding which is which makes all the difference.
Decoding the Compound Interest Formula
After seeing the snowball effect in action, you can feel why your money grows faster with compounding. Now, let’s peel back the curtain and look at the "how." The engine behind this financial magic is a single, powerful equation.
At first glance, the compound interest formula might look a little intimidating. Don't worry. It's really just a precise recipe for figuring out your future wealth. Let's break down each piece, turning it from a jumble of letters into a tool you can actually use.
The formula is A = P(1 + r/n)^(nt). Think of it as the mathematical blueprint for growth. It calculates A (the final amount) you'll have after a certain number of years.
Meet the Characters in the Formula
The best way to understand the formula is to think of it as a cast of characters. Each one plays a critical role in your investment's story. Getting to know them is the key.
Here are the main players:
- A = The Final Amount: This is the grand total in your account when the term is up. It’s your original money plus all the interest it’s earned along the way.
- P = The Principal: This is your starting cash. It's the initial lump sum you deposit into a savings account, CD, or other investment.
- r = The Annual Interest Rate: This is the growth rate your money earns over a year. Critically, you have to write it as a decimal for the math to work. So, a 5% rate becomes 0.05.
- n = The Compounding Frequency: This number shows how many times per year the interest gets calculated and added back into your principal.
- t = Time in Years: This is simply how many years you plan to let your money cook.
Key Insight: Each variable in the formula represents a lever you can pull. You control the Principal (how much you start with) and Time (how long you invest). You can shop around for the best Rate and Compounding Frequency.
Why Each Variable Matters
Each of these components directly impacts your final balance, ‘A’. Let's dig into what each one actually does inside the equation.
Principal (P)
Your principal is the foundation. It's the "P" in A = P(1 + r/n)^(nt), and a bigger starting principal means every percentage gain translates into more real dollars from day one. It gives your interest something substantial to build upon.
Annual Interest Rate (r)
The rate, or ‘r’, is your growth engine. A higher rate means your money grows faster. Just remember to convert the percentage to a decimal. For instance, a 4.25% APY becomes 0.0425 in your calculation. To see how different rates can change your outcome, play around with our free compound interest calculator for CDs.
Compounding Frequency (n)
This is where the real magic kicks in. The value of ‘n’ simply depends on how often your interest is paid out and added back to the balance.
- Annually: n = 1
- Quarterly: n = 4
- Monthly: n = 12
- Daily: n = 365
The more often interest is compounded, the sooner your earned interest starts earning its own interest. This creates a slightly faster—and more profitable—growth curve.
Time (t)
Time is, without a doubt, the most powerful multiplier in the formula. Notice that ‘t’ is part of the exponent. That means its impact isn't linear—it's exponential. The longer you let your money grow, the more dramatic that snowball effect becomes, making time your single greatest ally in building wealth.
How Time and Frequency Fuel Your Growth
Of all the variables in the compound interest formula, two have a much bigger impact on your final balance than you might think: time (t) and compounding frequency (n). While your initial deposit and the interest rate set the stage, these two factors are the real accelerators. They are what turn slow, steady gains into a steep, rewarding curve.
Let's put them under the microscope.
Imagine you have $1,000 to put into an account that pays a 5% annual interest rate. How much difference can the compounding schedule really make? It all comes down to how often the bank calculates your interest and adds it back to your principal.
The Power of Compounding Frequency
The more often your interest is compounded, the faster your money starts working for you. It's a subtle but powerful effect. Each time interest is added, your principal gets a tiny bit bigger, so the next interest calculation is based on that slightly higher balance.
Let's run the numbers on that $1,000 investment at a 5% rate over 10 years, changing only the compounding frequency (n):
- Compounded Annually (n=1):
A = 1000(1 + 0.05/1)^(1*10) = $1,628.89 - Compounded Quarterly (n=4):
A = 1000(1 + 0.05/4)^(4*10) = $1,643.62 - Compounded Monthly (n=12):
A = 1000(1 + 0.05/12)^(12*10) = $1,647.01 - Compounded Daily (n=365):
A = 1000(1 + 0.05/365)^(365*10) = $1,648.66
As you can see, switching from annual to daily compounding adds nearly $20 over the decade. It's not a fortune, but it's free money you get just by choosing an account with a more frequent schedule. You can dive deeper into how these schedules stack up in our guide on the differences between daily and monthly compound interest.
The Real Superpower: Time
While a higher frequency gives you a nice little edge, time is the undisputed champion of building wealth. It's the 't' in the exponent of the formula, (nt), meaning its impact is exponential. Nothing else has the same raw power to turn small savings into serious money.
Let’s stick with our $1,000 principal and 5% interest, compounded annually. This time, we’ll just change the time horizon.
Key Takeaway: The longer you let your money sit and compound, the more dramatic the growth becomes. The interest you earn in the later years will eventually dwarf the interest from the early years.
This infographic shows how that growth starts to pick up speed.
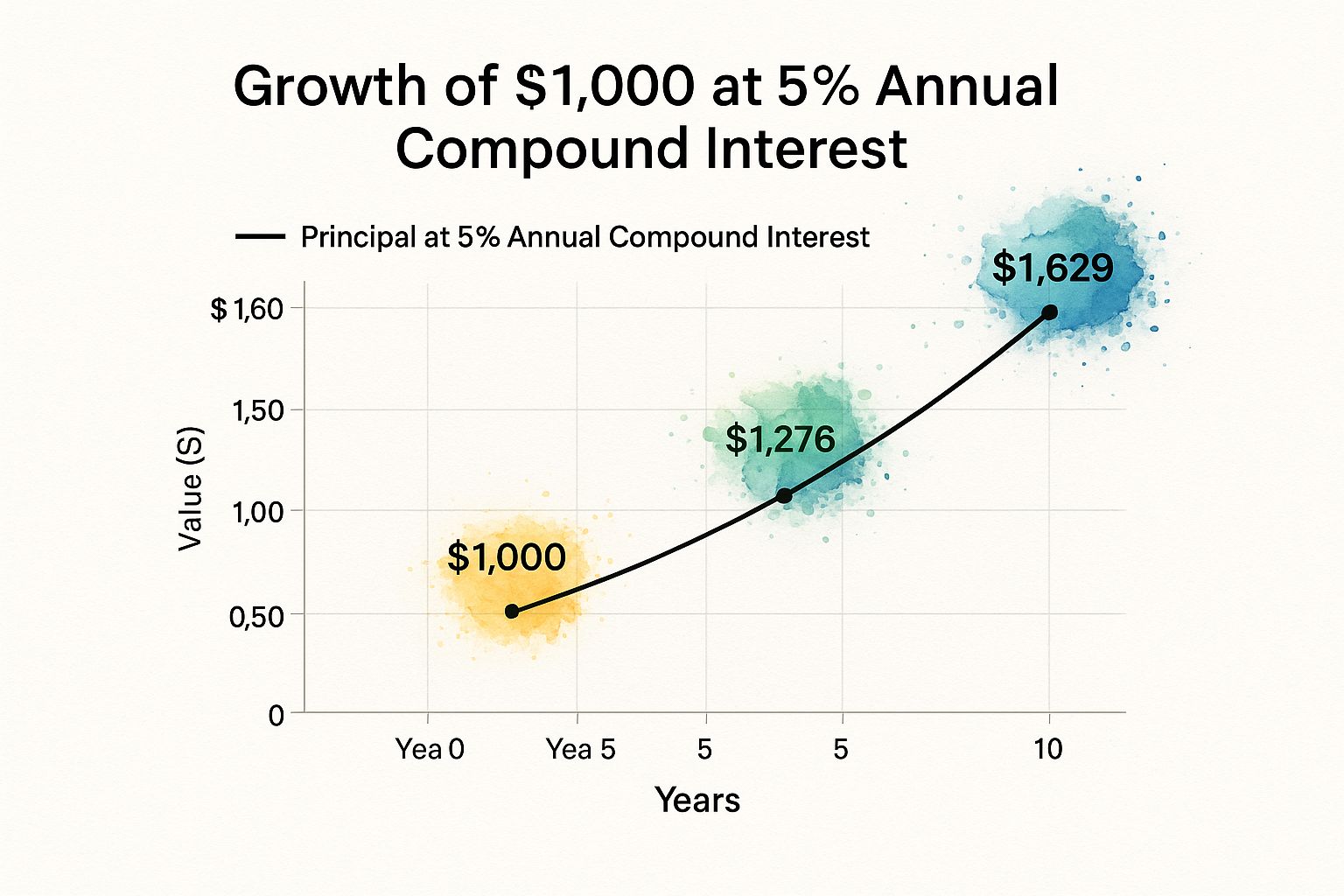
You can clearly see that the growth in the second five years is bigger than in the first five. That’s compounding in action.
Now, let's really stretch the timeline to see the magic happen.
Growth of $1,000 at 5% Annual Interest
| Time (Years) | Final Amount | Total Interest Earned |
|---|---|---|
| 10 Years | $1,628.89 | $628.89 |
| 20 Years | $2,653.30 | $1,653.30 |
| 30 Years | $4,321.94 | $3,321.94 |
| 40 Years | $7,039.99 | $6,039.99 |
Look closely at those numbers. It took 10 years to earn the first $629 in interest. But it only took the next 10 years to earn another $1,024. By the fourth decade, that initial investment was churning out over $2,700 in interest alone.
This is exactly why financial experts always say the single most important thing you can do is start early. The years you aren't invested are years of compounding you can never get back.
While we often think of compounding in terms of savings growth, understanding variable rates in loan products can also highlight the importance of time and interest. For example, learning the mechanics of adjustable rate mortgages offers another angle on how interest calculations change over a product's life, reinforcing the powerful role these variables play. When time is on your side, the results are incredible; when it's working against you in debt, the impact can be just as potent.
Putting the Formula to Work in Real Life

This is where the rubber meets the road. Knowing the formula is one thing, but seeing how it plays out with real money is what makes the concept of compound interest click. The math isn’t just some abstract theory; it's a force that's actively shaping your financial future, whether you’re saving or borrowing.
Let's walk through three different scenarios. We’ll use the same core formula—A = P(1 + r/n)^(nt)—and just swap out the numbers. You’ll see exactly how it can build your savings, inflate your debt, or secure your retirement.
Example 1: Growing a High-Yield Savings Account
High-yield savings accounts are a fantastic, low-risk tool. They're perfect for an emergency fund or short-term goals because they almost always compound interest daily, giving your cash a small but meaningful advantage over traditional savings.
Let’s say you open an account with $5,000 that pays a 4.0% interest rate, compounded daily. You don't touch it for five years.
Here’s our setup:
- P (Principal): $5,000
- r (Rate): 0.04 (4.0% as a decimal)
- n (Compounding Frequency): 365 (for daily)
- t (Time): 5 years
Plugging those into the formula gives us:
A = 5000 * (1 + 0.04 / 365)^(365 * 5)
A = $6,106.99
Without lifting a finger, your original deposit grew by $1,106.99. This is the quiet power of putting your money to work. Online tools, like the CD calculator in the image above, let you run these numbers in seconds. You can plug in your own deposit, rate, and term to see a clear visual of how your money will grow over time.
Example 2: The High Cost of Credit Card Debt
The compound interest formula is impartial; it works the same way on debt, and the results are painful. When you carry a credit card balance, the bank is using compounding against you.
Imagine a $3,000 credit card balance with a 21% APR. Most cards compound daily. Let's see what happens if that balance just sits there for one year, with no payments made.
- P (Principal): $3,000
- r (Rate): 0.21
- n (Compounding Frequency): 365
- t (Time): 1 year
Running the calculation:
A = 3000 * (1 + 0.21 / 365)^(365 * 1)
A = $3,702.43
In only 12 months, that $3,000 debt has snowballed by over $700. You're not just paying interest on the initial $3,000—you're paying interest on the interest that gets tacked on every single day.
Critical Takeaway: This is precisely why making only minimum payments on high-interest debt feels like running in place. Most of your payment gets eaten by interest charges, barely touching the principal. Grasping this math is the first step toward building a real strategy to crush high-APR debt.
Example 3: Projecting Your 401(k) Retirement Growth
Now for the fun part. This is where compounding shows its truly life-changing potential. Retirement accounts like a 401(k) or IRA are built for the long haul, giving your investments decades to grow. The results can be incredible. Long-term savings vehicles, including superannuation and its growth potential, rely heavily on this principle.
Picture a 25-year-old who has $10,000 saved in their 401(k). We'll assume a 7% average annual return, compounded once a year, and see where it lands by age 65. (To keep it simple, we'll ignore any new contributions and just watch this single sum grow).
The variables for our final scenario:
- P (Principal): $10,000
- r (Rate): 0.07
- n (Compounding Frequency): 1 (annually)
- t (Time): 40 years
Let's put it all together:
A = 10000 * (1 + 0.07 / 1)^(1 * 40)
A = $149,744.58
That one-time $10,000 investment, left alone over a career, could become nearly $150,000. It didn't just grow; it multiplied. A staggering $139,000 of that final amount is pure profit from compounding. It’s the ultimate proof that when it comes to investing, time is your most powerful ally.
The Surprising History of Compound Interest
The compound interest formula might feel like a slick, modern financial invention, but its core principle is actually an ancient secret. For thousands of years, it’s been quietly shaping economies, long before spreadsheets and calculators ever existed.
The story starts not in a bank, but on a farm. Some of the earliest recorded examples of compounding pop up in Sumerian and Babylonian records around 2000 BCE. Scribes would carefully track loans of seeds and livestock. If a farmer borrowed grain, the interest was paid back in more grain. That extra grain was then added to the original amount and loaned out again. It was compound interest in its most basic, agricultural form. You can dig into some of the historical details on these early financial practices on Wikipedia's page on compound interest.
From Farmlands to Formal Law
As civilizations got more complex, so did their money. The idea traveled to the Roman Empire, where it became a hot topic of legal and philosophical debate. Roman law actually tried to outlaw interest on interest through the lex Genucia, seeing it as a way to exploit people. This gets at a timeless tension: right from the start, people recognized compounding's incredible power, both to build fortunes and to bury borrowers in debt.
But despite the moral arguments, the math was just too powerful to ignore. Fast forward to the Italian Renaissance, and the concept got a major upgrade. Florentine merchants—the masters of trade and finance back then—created the first formal interest tables. These tables were critical tools, letting them accurately project the future value of loans and investments. They were laying the groundwork for modern banking.
Key Historical Insight: The discovery of the mathematical constant 'e' (the one that's roughly 2.718) is tied directly to compound interest. In the 17th century, the mathematician Jacob Bernoulli was trying to figure out what would happen if you compounded interest an infinite number of times. His work on this very problem of continuous compounding led him straight to 'e', a number that is now fundamental to science and finance.
A Timeless Economic Principle
The long, winding history of compound interest tells us something important: it’s more than just a formula. It’s a fundamental law of growth that different cultures have discovered and used over and over again for millennia. From ancient clay tablets tracking barley loans to the high-speed algorithms running our financial markets today, the core concept hasn't changed.
When you grasp this history, you realize you're not just plugging numbers into a calculator. You're tapping into a force of economic momentum that has a 4,000-year track record. This is the very same principle that makes your savings account or a Certificate of Deposit grow. If you're curious about how this ancient idea works in a modern savings tool, we have a thorough explanation of a Certificate of Deposit here. The tools are new, but the snowball effect is as powerful as ever.
Common Questions About Compound Interest
Now that you've seen the compound interest formula in action, you probably have a few practical questions bubbling up. It’s one thing to see the math play out with examples, but it's another to feel ready to apply it to your own financial life.
Let's tackle some of the most common questions that come up. Think of this as the practical advice that bridges the gap between theory and your wallet.
What Is the Rule of 72?
The Rule of 72 is one of the most useful bits of financial shorthand you'll ever learn. It's a quick, back-of-the-napkin trick to estimate how many years it will take for an investment to double, all thanks to compounding.
No calculator needed. Just divide 72 by the annual interest rate. The answer is a surprisingly close estimate of how long it takes for your money to double.
For instance, if your investment earns an average of 8% per year, the math is simple:
72 ÷ 8 = 9
That tells you it will take about 9 years for your investment to double. It's a fantastic mental shortcut that works best for interest rates you’d typically see in finance, usually between 6% and 10%.
The Rule of 72 in Action: It perfectly illustrates the trade-off between risk and time. An investment earning a safe 4% return will take roughly 18 years to double (72 ÷ 4). Meanwhile, a riskier investment pulling in 12% could double in just 6 years (72 ÷ 12).
Can I Use This Formula for My Credit Card Debt?
Yes—and you absolutely should. The math of compound interest is impartial. It works the same way for debt as it does for savings, which is precisely why high-interest debt can feel so crushing. It reveals just how fast the hole you're in can get deeper.
When you're looking at debt, the formula's variables just take on a darker meaning:
- P (Principal): Your outstanding credit card balance.
- r (Rate): Your card's Annual Percentage Rate (APR).
- A (Final Amount): The total you will owe after a set period if you make no payments.
For most credit cards, the compounding frequency (n) is daily. Every single day, a tiny bit of interest is calculated and tacked onto your balance. The next day, you’re paying interest on that new, slightly higher balance. This is why making only minimum payments can feel like running on a treadmill—the interest charges often grow faster than your payments chip away at the principal. Understanding this is the first step to getting out of that cycle.
What’s the Difference Between APR and APY?
This is one of the most critical distinctions in all of personal finance. They sound almost the same, but APR and APY tell you very different stories about your money.
APR (Annual Percentage Rate) is the simple, base interest rate for one year. It's the "sticker price" of interest and does not include the effects of compounding that happen within the year.
APY (Annual Percentage Yield) is the rate you actually earn or pay because it does include the effect of compounding. If an account compounds interest more than once a year (like daily or monthly), the APY will always be a bit higher than the APR.
Here’s a simple way to think about it:
| Feature | APR (Annual Percentage Rate) | APY (Annual Percentage Yield) |
|---|---|---|
| What It Includes | The base annual interest rate only. | The annual interest rate plus the effect of compounding. |
| When It's Used | Often quoted for loans and credit cards to show the base cost of borrowing. | Used for savings accounts and CDs to show your true, effective return. |
| Which Is Better? | A lower APR is better when borrowing. A higher APY is better when saving. |
When you're saving, you want the highest APY you can find—it means more money in your pocket. When borrowing, the APR is the starting point, but the compounding is what determines the true, total cost.
How Do I Calculate Growth with Monthly Contributions?
The standard formula, A = P(1 + r/n)^(nt), is perfect for a single, lump-sum investment that you just set and forget. But that's not how most of us save. We add money regularly, like contributing to a 401(k) from every paycheck or moving money into savings each month.
When you add regular deposits, the math gets a lot more complex. You need a different formula, often called the "Future Value of a Series" or "Future Value of an Annuity."
But you don't need to dust off an old textbook. Modern tools are built to handle this for you.
- Online Investment Calculators: Tools like our CD Calculator and others are designed for exactly this. You can plug in your starting amount, monthly contribution, rate, and timeline to get an instant, accurate picture.
- Spreadsheet Software: Programs like Microsoft Excel or Google Sheets have this built-in. The
=FV()function does all the heavy lifting to calculate the future value of an investment with regular payments.
The key takeaway is that while the underlying math is trickier, the principle is the same. Consistent contributions turbocharge the power of compounding, creating a much steeper growth curve than a single deposit ever could on its own.
Ready to see how different rates and regular deposits could impact your own goals? Use the free BankDepositGuide.com Certificate-of-Deposit Calculator to run your own numbers and get a clear picture of your money's future.